The Mean Value Theorem (MVT or short) is among the most popular subjects in the mathematics education literature. It is one of the key tools available to mathematicians that can be employed to prove a myriad of other theorems related to Differential and Integral Calculus. In addition, it is often developed as a result of its particular case, “Roll’s theorem. It is named for Michel Rolle (1652-1719), a French mathematician who developed the widely used symbol of the number nth. He demanded that -a = -b for both positive a and b and equal the a and b. This was in direct contradiction to Descartes the way he taught and laid the foundation for creating the popular number line.
Mean Value Theorem
Mean Value Theorem is a significant mathematical theorem. The first version of the theorem of mean values was suggested during the 14th century Parmeshwara Mathematical Scientist from Kerela, India. Rolle presented a simpler version in the 17th century, namely, The Theorem of Rolle, which was only proved for polynomials and was not included in the calculus. Augustin Louis Cauchy proposed the current variant of the Mean Value Theorem in 1823.
Mean value says that for a curve running through two specified points, there exists a point in the angle at which the tangent is parallel to the secant that passes through the two points. The theory of Rolle was derived from this theorem of the mean value.
The Mean Value Theorem and Its Meaning
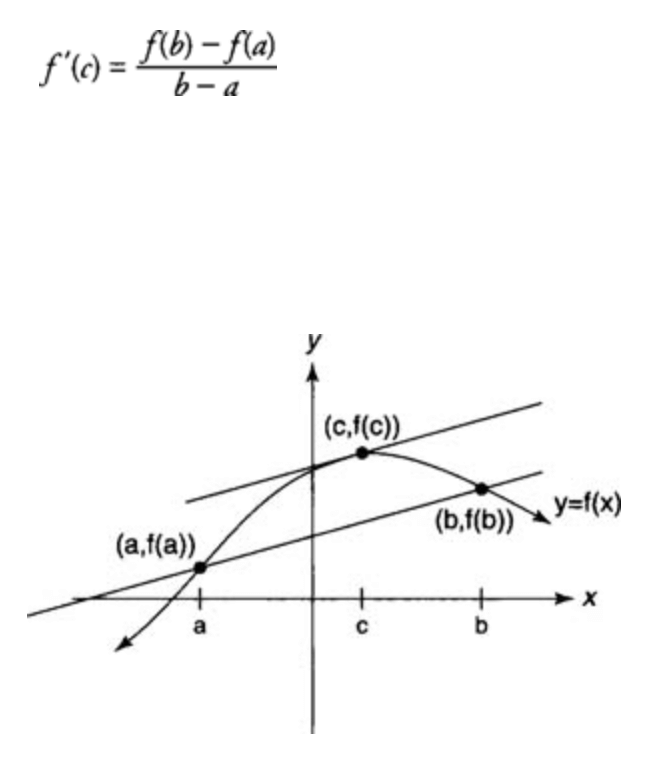
The theory of Rolle is a particular version of the Mean Value Theorem. In Rolle’s Theorem, we take into consideration the differentiable function f, which are defined as an enclosed interval [a,b] where f(a)=f(b). The Mean Value Theorem generalizes Rolle’s theorem by looking at functions that do not necessarily have the same value at the ends. In this way, we can think of this Mean Value Theorem is a slanted version of the theory (Figure 4.25). This Mean Value Theorem states that if it is continuous over an open interval (a and b) as well as differentiable across an open space (a,b), in which case there is an element c(a,b) in which the tangent line of the graph of the f at c runs parallel with the second line connecting (a,f(a)) with (b,f(b)).

For more information and assistance, visit the following websites.
https://en.wikipedia.org/wiki/Mean_value_theorem
https://tutorial.math.lamar.edu/Classes/Calci/MeanValueTheorem.aspx
https://courses.lumenlearning.com/suny-openstax-calculus1/chapter/the-mean-value-theorem/
https://www.cliffsnotes.com/study-guides/calculus/calculus/applications-of-the-derivative/mean-value-theorem
https://math.libretexts.org/Bookshelves/Calculus/Map:Calculus__Early_Transcendentals(Stewart)/04:Applications_of_Differentiation/4.02:_The_Mean_Value_Theorem https://math.libretexts.org/Bookshelves/Calculus/Book:_Calculus(OpenStax)/04:_Applications_of_Derivatives/4.04:_The_Mean_Value_Theorem
https://www.cuemath.com/calculus/mean-value-theorem/
https://www.cut-the-knot.org/Curriculum/Calculus/MVT.shtml
https://openstax.org/books/calculus-volume-1/pages/4-4-the-mean-value-theorem
https://math.dartmouth.edu/~m3cod/ionescuslides/Lecture12.pdf